Sistemas de conversión

- Definición: «En informática, la conversión alude al proceso de transformación de datos informáticos de una representación concreta a otra, cambiando los bits de un formato de archivo formato a otro, normalmente para lograr la interoperabilidad de aplicaciones o sistemas diferentes». Al nivel más simple, la conversión de datos puede ejemplificarse por la conversión de un archivo de texto desde una codificación de caracteres a otra. Son conversiones más complejas las de los formatos de ficheros ofimáticos y multimedia, a veces fuera de las capacidades de ordenadores domésticos (o a expensas de tiempos de proceso muy altos).

- Procedimiento para hacer conversiones de números decimales a binarios.

Para hacer la conversión de decimal a binario, hay que ir dividiendo el número decimal entre dos y anotar en una columna a la derecha el resto (un 0 si el resultado de la división es par y un 1 si es impar).

- Dividir entre 2 sucesivamente.

- Apuntar el resultado y el resto de cada operación.

- Apuntar a lista de ceros y unos de abajo a arriba.

Ejemplos: 

1. Vamos a pasar a binario 79₁₀

79/2=1 (impar). 

39/2=1 (impar). 

19/2=1 (impar). 

9/2=1 (impar).

4/2=0 (par). 

2/2=0 (par). 

1/2=1 (impar).

Por tanto, 7910 = 1001111.

2. Por ejemplo el número decimal 23519:

23519 / 2 = 11759 Residuo: 1

11759 / 2 = 5879 Residuo: 1

5879 / 2 = 2939 Residuo: 1

2939 / 2 = 1469 Residuo: 1

1469 / 2 = 734 Residuo: 1

734 / 2 = 367 Residuo 0

367 / 2 = 183 Residuo: 1

183 / 2 = 91 Residuo: 1

91 / 2 = 45 Residuo: 1

45 / 2 = 22 Residuo: 1

22/ 2 = 11 Residuo: 0

11 / 2 = 5 Residuo: 1

5 / 2 = 2 Residuo: 1

2 / 2 = 1 Residuo: 0

1 / 2 = 0 Residuo: 1

Acomodando los residuos en orden inverso el número decimal 23519 sería el 101101111011111 binario.

- Procedimiento para hacer concesiones de números binarios a decimal.

El proceso inverso para convertir un número binario a decimal es aún más sencillo.

Basta con numerar los dígitos de derecha a izquierda comenzando desde cero, a cada número se le asigna la correspondiente potencia base 2 y al final se suman las potencias.

1. Por ejemplo el número binario 10101100 a decimal sería:

• 0 * 20 = 0
• 0 * 21 = 0
• 1 * 22 = 4
• 1 * 23 = 8
• 0 * 24 = 0
• 1 * 25 = 32
• 0 * 26 = 0
• 1 * 27 = 128

Sumando los resultados de las potencias:

0 + 0 + 4 + 8 + 0 + 32 + 0 + 128 = 172

Por tal, el número binario 10101100 es el 172 decimal.

2. Ejemplo el número 1001 queremos saber su equivalente en decimal. Primero asignamos exponentes:

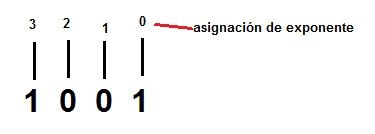
Empezamos por el primer producto, que será el del primer número binario por 2 elevado a su exponente, es decir 1 x 23 . OJO Recuerda que cualquier número elevado a cero es 1, por ejemplo 2 elevado a 0 es = 1.

El segundo y el tercer productos serán 0 por que 0 x 22 y 0 x 21 su resultado es 0 y el último producto será 1 x 20 que será 1, luego 1 x 20 es 1 (no confundir y poner 0). Ya estamos en el último paso que es sumar el resultado de todos estos productos:

1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 8 + 0 + 0 + 1 = 9

El equivalente en decimal del número binario 1001 es el 9.

-Video de apoyo: 
1. [Método Fácil] Convertir de Binario a Decimal y viceversa: https://www.youtube.com/watch?v=c-hyLLdDt7I 

Binario a Decimal---Minutos: 0:00 a 8:52.

2. CONVERTIR de DECIMAL a BINARIO https://www.youtube.com/watch?v=fGu0tM5u4b4

Referencias:

1. https://es.wikipedia.org/wiki/Conversi%C3%B3n_(inform%C3%A1tica)

2. http://recursostic.educacion.es/secundaria/edad/4esotecnologia/quincena5/4q2_contenidos_2c.htm

3. https://ed.team/blog/sistemas-binarios-y-decimales

4. https://www.areatecnologia.com/sistema-binario.htm